leetcode_63

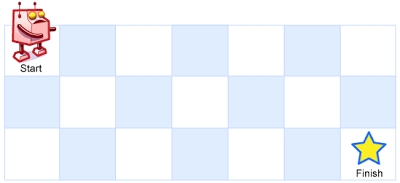
A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).

The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).

Now consider if some obstacles are added to the grids. How many unique paths would there be?

a

An obstacle and empty space is marked as 1 and 0 respectively in the grid.

Note:

m and n will be at most 100.

Example 1:

Input:
[
  [0,0,0],
  [0,1,0],
  [0,0,0]
]
Output: 2
Explanation:
There is one obstacle in the middle of the 3x3 grid above.
There are two ways to reach the bottom-right corner:
1. Right -> Right -> Down -> Down
2. Down -> Down -> Right -> Right

Solutions

1. Dynamic programming

class Solution {
public:
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
        if (obstacleGrid[0][0] == 1) return 0;
        int m = obstacleGrid.size(), n = obstacleGrid[0].size();
        long dp[n]; for (int i = 0; i < n; i++) dp[i] = 0;
        for (int i = 0; i < n && !obstacleGrid[0][i]; i++) dp[i] = 1;
        bool prex = false;
        for (int i = 1; i < m; i++) {
            if (obstacleGrid[i][0]) dp[0] = 0;
            for (int j = 1, prex = true; j < n; j++) {
                if (obstacleGrid[i][j] == 1)
                    dp[j] = 0;
                else
                    dp[j] = dp[j - 1] + dp[j];
                if (dp[j]) prex = false;
            }
            if (prex) return 0;
        }
        return dp[n - 1];
    }
};